KEYWORDS: alignment of sequences, "motif” alignment, dynamic programming, iterative method, WWW.

In the article [1] there were described methods of iterative dynamic improvement of initial alignment (see below #2). In it, as a “priming” (the initial alignment) was taken either a trivial alignment, for which all sequences were moved to the left, or an alignment, created by a cluster algorithm Clastal V [3].

In the article [2] we offered an algorithm of building the “motif” multiple alignment of biological sequences. This article states that the motif alignment acts like a good “priming” with iterative dynamic improvement of an alignment. Most likely, this happens because in the motif alignment there are “embryo” of sub-optimal positions present [4]. The use of iterative algorithm in case of motif alignment transforms these “embryos” to sup-optional positions, at the same time destroying the false homology columns positions, that compete with the sub-optional ones.

In the beginning we described the methods of motif alignment building and iterative dynamic improvement of the “priming”. As the article goes on, the work of the algorithm will be demonstrated using it as applied to “true” alignments restoration. As “true” alignments there were taken ether biologically-based ones, or alignments built using an artificial computer “mutation” process. There will be introduced values, describing the quality of “true” alignment’ restoration and there will be mentioned results, showing how this quality depends on the kind of the “true” alignment itself, and the chosen “priming”.

MATERIALS AND METHODS

Motif alignment. In the motif alignment method in the beginning there are “MOTIFS” [2]; each of these “motifs” consists of fragments of the same length (without gaps) from different sequences of source set. These fragment are similar and are put against each other. After that from these “motifs” is an alignment composed, which is a chain of matched (looking on the order of letters in the sequence) motifs, in between which there is a needed a number of gaps.

The quality of an alignment could be valued either by percent of homologies - by the sum of weights of residue exchange per one alignment position or so-called POWER [5,6] ( with of power definition, coming from probabilities theory arguments, the sum of weights is divided not by length, like in the case of homology percent, but by the square root of the length).

Method of iterative dynamic improvement of multiple alignment. In this article we are using the simplest method of iterative dynamic improvement of an alignment, that does the following [7]. Say there is a certain amount of sequences and there is a certain initial alignment (“priming”) combined out of those. The lines of the priming alignment (sequences) are taken by turns. On each step the next sequence is removed from an alignment and then, using the method of pair dynamic programming, this sequence is aligned against a part-that-is-left of the alignment. The resulted alignment is used in the next step. This is done until the quality of an alignment doesn’t increase, when going through all the lines of an alignment. Here the quality of an alignment is measured by two parameters: it’s power and the homology percent, so that on each step both parameters should increase: simultaneously.

In [1] more complicated variants of iterative dynamic improvement of an alignment are described. They are concerned with dividing a set of sequences of the initial alignment to two sub-sets at each step. These methods are much more labor-consuming. At the same time, even the simplest variant works satisfactorily in case of right-built priming.

“True” alignments. As it was mentioned before, in the restoration procedure as “true” alignments, the “biologically right” ones, as well as, ones got using modeling of mutation process were taken.

Biologically right alignments were considered the ones that either are considered of that sort by expert-biologists, or correspond with alignment of tertiary protein structures.

Artificial examples, on which there was this method tested, were built using the following computer “mutation” process. There was one sequence selected ( say it was selected randomly). Then this sequence was repeated several times. Thus the alignment was created. It was composed of a certain number of the same sequences. Then, with this identical alignment the mutation procedure was made. It is composed of the following: in some probabilities letter substitutions and deletions were made, deletion is substituting a letter with space. Altogether talking, these probabilities of substitutions depended on the column number and sequence number several of such dependencies were investigated. The important characteristic of the mutational process is it’s duration - the amount of mutations/deletions calculated per one position of an alignment.

The quality of restoration. As the main characteristic of restoration quality taken the following value was taken: standardized number of pairs of letters differences of the “true” and built alignments.

Except for this value, estimating the quality of restoration of the true alignment, we also took into an account how good the “sub-optimal strong” columns restored. “Strong columns” means that to these columns corresponds with a big sum of weights letter substitutions. “Sub-optimal” means the following [4]. We fix the given column and make the best possible alignment to the left of this column, that is those sequence parts are aligned, that are to the left of this column. The same is done to the right of this column. As a result we get a full alignment, containing the given column as a whole. (The approximation to this best alignment is iterative improvement of the corresponding “motif” alignment). After this a small vicinity of the studied column of the alignment is taken. Parts of an alignment, to the right and to the left of the vicinity are fixed, and the vicinity itself is improved by dynamic, iterative method (this is also an approximation of the best alignment within the vicinity). If the studied column was not destroyed (or almost saved), then this column is called sub-optimal.

The quality of restoration of an alignment, that was described before, we calculated not only by all the columns, but also separately by sub-optimal, strong columns (it seems, the last value is more accurate).

Dependence of the “true” alignment’s restoration from the initial alignment (“priming”). As it was said before, both the homology percent of the resulting alignment and the quality of the “true” alignment’s restoration with the procedure of iterative dynamic improvement strongly depend on the priming.

To check this dependence we used primings of several types. One of them - trivial priming alignment - move of all sequences to the least left position so that all gaps would be on the right. The second type of priming - “motif” aligning. The third type of priming is a result of the “true” alignment damage. It consists of the following: with certain possibilities the fragments of gaps of different length are included in or excluded out of the sequences, involved in the true alignment,. The smaller are these possibilities, the smaller is the “damage”.

The results of the work are shown on the tables 1-6 and pictures 1-2. They point out the restoration quality in the procedure of iterative dynamic improvement of an alignment for different kinds of priming.

Each table refers to definite series of computer experiments. Usually, series are made of 30 calculations of the same kind.

The results of computer mutations are shown on the tables 1-4.

On the tables 1-3 the scheme of mutational process is as following. There are 10 sequences of length 50 in a resulting alignment. All of the alignment positions (columns) were divided into two zones. First zone consists of the first 40 positions, the second one - of the last 10. In the first zone probability of mutations (that is letter changes) is equal to p₁, for the second one - p₂ , and probability of deletion (that is crossing out of letters) is, accordingly, q₁ and q₂. For each tables 1-3 there is a composition of probabilities p₁, p₂, q₁, q₂.

Each of the lines of the tables1-3 has its definite kind of priming. For the first line of the table the priming coincides with the true alignment. For the next 6 lines the priming is “damaged” true alignments. The “damage” consists of cutting out or adding , randomly, some amount of gaps. In the second line of each table all gaps are excluded(that is those are trivial alignments) , in the third line part of the gaps that were excluded is equal to about 0.66, in the forth- 0.33. In the lines 5, 6 and 7 gaps were included. The last line of the tables corresponds with the case when the priming was taken as the motive alignment.

Note: Here and in all following tables the following signs are used:

Tables 4, 5 and 6 consist of 3 lines , first line corresponds with the case of true alignment as the priming , second line - damaged true alignment ( extra gaps were included) , third line - when priming is a motive alignment.

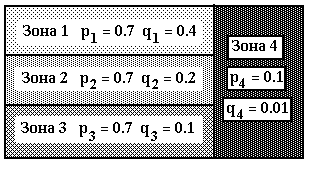
For the table 4 the other scheme of mutational process with 4 zones, that are shown on the picture 1. Here the overall number of consequences is equal to 12. Each of the zones 1, 2, 3 consist of 4 consequences and 40 positions . Zone 4 consists of 10 last positions in each of the 12 consequences. Each zone is characterized by its composition of mutational parameters p_i, q_i = 1, 2, 3, 4, where p_i - possibility of mutation, and q_i - possibility of deletion ( see picture1 ).

The composition shows that motive alignment as priming is the winner in the quality of the restoration of the true alignment.

Tables 5-6 are analogues to tables 1-3, however they relate to the accident, where as true alignments the biologically approved alignments were taken. In the table 5 that kind of alignment was constructed by biologist-expert. In the table 6 the true alignment corresponds with the alignment of tertiary structure of proteins.

Table 6. The true alignment corresponds with the alignment of tertiary structure of proteins

Picture 1. Zones for mutational procedure, that corresponds with tables 4 .Here: p_i, q_i - possibilities of mutations and deletions in zone i.

On the pic. 2 the graphs that characterize the quality of restoration of the alignment, according to the quality of restoration of the columns of priming are shown.

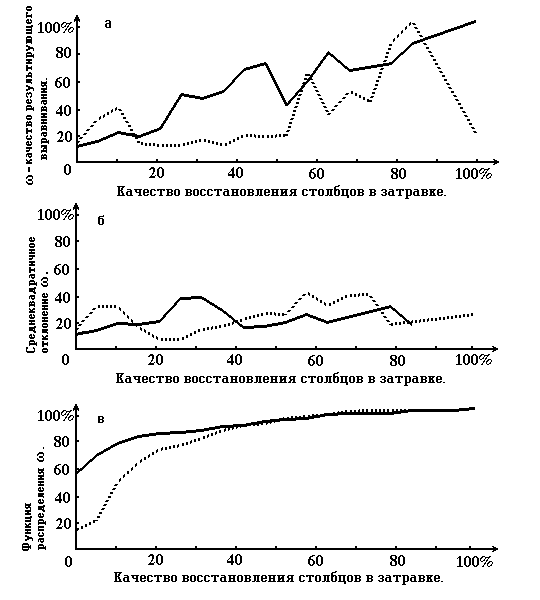
Picture 2. Graphs that characterize the quality of restoration of the resulting alignment according to the quality of restoration of the priming’ columns (see paragraph 4). On the abscissa axis for all 3 graphs the quality of true alignment column restoration in priming is measured. On the ordinate axis of graph 2a the quality of resulting alignment, on the graph 2b - root-mean-square deviation, on graph 2c - functions of distribution of columns of the priming restoration quality. The solid line shows the case, when motif alignment is the priming, dotted line - one of the cases of damaged true alignment (when gaps are included).

Picture 2 corresponds with Table 3 .

The outcome of the work is as follows:

The methodology how to estimate the quality of restoration of the columns of the true alignment is proposed. This methodology can be used to compare different methods of alignment construction. At given work it was used for investigating the iterative dynamic improvement of the motive alignment.

From the results we can see that the usage of the priming motive alignment improves the quality of restoration. Especially this is true for the “good” columns of priming - those that do not strongly differ from the corresponding columns of the true alignment . This is characterized , for example, by the picture 2a. The graph there corresponds with the motive alignment. On the right part of the picture it is higher than the graph for damaged priming and even higher than the diagonal. Vice versa , on the left side of the picture ( that response to small level of correspondence of the columns of the priming and the true alignment) the quality of the restoration of the motive priming is lower then for the damaged. However this, from our point of view, is not a minus , because the method is not claiming to restore strongly destroyed columns.

It’s necessary to mention that the restoration of so called “suboptimal” columns of the true alignment [4] is better than also strong, but not “suboptimal” columns.

Authors highly appreciate to Dr. Alexander E. Gorbalenya for the help in choosing biological examples.

The work was supported by grant 95-07-19298 of Russian Foundation for Basic Research.